[데이터사이언스개론] Chapter 4

modeling

• predictive modeling (predictive accuracy)
  • mathematical expression : linear regression/parametric modeling → chap 4
  • logical statement or rules : decision tree/ nonparametric modeling → chap 3
• descriptive modeling (intelligibility or understandability)
  • clustering, profiling

---

Predictive Modeling 의 type

Nonparametric modeling Parametric modeling

구조	정해지지 않음	정해짐
	데이터에 따라 정해짐	데이터 애널리스트가 정함

---

Nonparametric Modeling

: 구조를 정하지 않고 데이터로부터 배운다. (classification tree) - chap 3에서 배움.

---

Parametric Modeling (parameter learning)

• 접근 방법
  1. 정해지지 않은 파라미터로 모델의 형태를 정한다.
  2. 학습데이터를 바탕으로 최적의 파라미터를 구한다.
• 모델의 형태는 domain knowledge나 다른 데이터 마이닝 기술로 정해진다.
• 목표: 최적의 파라미터 값을 찾는 것

 

	classification tree	linear classifier
space partition	축으로 나눔	아무 각도로 가능
지역 분리	여러 지역 나옴	두 지역만 나옴
가중치	가중치 없음	가중치 있음
형태	IF () AND () THEN Class=	IF(수식>0) THEN Class=

---

General Linear Classifier

w0, w1, w2.. 가 파라미터일 때 f(x) = w0 + w1x1+ x2x2+ … + wnxn

• shape of decision boundaryn=3: 평면
• n=2: x축 y축
• 목표: 학습데이터를 바탕으로 최적의 w값들을 찾는 것
• 가중치
  • wi의 값이 클수록 중요하다고 본다.
  • 가중치 찾는 방법 (w 찾기)
    1. 목적함수(손실함수)를 정의한다.
    2. 가중치를 최대/최소화하는 최적값을찾는다.
  • 가중치 찾을 때 사용하는 목적함수
    • Support vector machine (SVM)
    • linear regression
    • logistic regression
    → 이 세 가지는 모두 같은 형태이지만 다른 목적 함수를 사용하기 때문에 w값이 다르다.

---

Support Vector Machine (SVM)

• 함수 형태: f(x) = w0 + w1x1+ x2x2+ … + wnxn
• SVM에서 최적의 직선: margin을 최대화시키는 직선 = 결정경계
• (두 클래스 모두로부터 멀리 있는 것이 제일 좋다. 잘 떨어뜨려놓으니까 안전하다.)
• Misclassification
  • 하나의 직선으로만 두 클래스를 완벽하게 분리시킬 수 없는 상황이 있다. 이럴 때는,
  • original objective function: 직선과 클래스 사이의 margin
  • new objective function: misclassification에 대해 penalty를 추가하자. → balance 유지
    • penalty의 값을 주는 기준
    • : 마진의 경계로부터의 거리 → hinge loss function

---

Linear regression

• 데이터를 가장 잘 설명하는 직선의 방정식 찾기 - 타겟 값을 예측하는 데 주로 사용
• 함수 형태: f(x) = w0 + w1x1+ x2x2+ … + wnxn
• 일반적인 과정
  1. 각각의 학습데이터(점)와 직선 사이의 거리인 에러값을 계산한다.
  2. 에러값 총합 내기
  3. 에러값의 총합을 최소화하는 w값들 찾기
• Least Squares Linear Regression : 에러값의 총합을 최소화하는 w값들 찾기 → 0으로 만들기
  •  

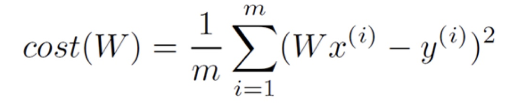
• 제곱 쓰는 이유: 에러값의 총합을 최소화하는 과정에서 여러 개의 값이 나올 수도 있고
• 정확한 값을 최소화시키기에는 수학적으로 w값들을 찾기 힘들다.
• 장점
  • 수학적으로 쉽고, unique solution을 생성한다.
• 문제점
  • 이상치가 있으면 직선의 방정식의 결과를 왜곡할 수 있다.
  • → 다른 목적함수들 존재

---

Logistic Regression

직선의 방정식으로 새로운 instance가 어떤 class에 속할지 확률을 추정할 때 사용

f(x) = w0 + w1x1+ x2x2+ … + wnxn의 범위가 무한대 → 확률에 쓰기 쉽도록 0~1로 범위 조정

• p(x)>0.5 : f(x)>0,
• p(x)=0.5: 결정 경계
• p(x)<0.5: f(x)<0

—> p(x)=1 → positive, p(x)=0 → negative

—> positive 하고 싶다면 p(x)는 1쪽으로 가야 하고 negative 하고 싶다면 0쪽으로 가야 한다.

 

---

Binary Classification

1. Linear classifier in binary classification

• 수식 설명: f(x)를 행렬로 표현하면 XW라고 할 수 있다. (행벡 열벡)

 

 

2. Logistic Regression in binary classification

 

---

Objective(Cost) Function

목적함수: 함수를 만들어서 함수값으로 학습이 잘 되었는지 확인한다.

Binary Classifcation에 주로 예시를 둔다. → target= 0 or 1

using logistic regression

1. Mean Square Error(평균제곱오차)

예측값과 실제값이 같으면 cost=0, 다르면 큰 값이 나온다.

그런데, 함수가 매끈하지 않고 미분 사용이 쉽지 않아서 적용하기 힘들다.

 

 

2. Cross Entropy

 

H(X)는 그대로 사용, log 함수에서 0과 1사이의 값만 사용한다.

 

---

Optimal W

w를 구할 때는 편미분을 사용한다.

• Gradient Descent Algorithm(최대경사법)
• 평균제곱오차인 경우) 편미분 값의 반대 방향으로 내려간다. 값이 감소하는 방향으로 진행한다.

a 값은 learning rate이다. a 값이 너무 크면 w에 수렴하지 않고 너무 작으면 오래 걸린다.

따라서 a 값을 적응적으로 준다.

 

cost function 에서..	linear regression	logistic regression
값의 범위 일치 여부	불일치	일치
값의 범위	넓음.	0~1 사이, 함수화 시키기 좋음
	H(X)=XW	H(X)=1/(1+e^(-f(x)))
H(X)==Y 이면	최저로	최저로
H(X)!=Y 이면	최대로	최대로

 

쉽게 누가 더 좋다고 말할 수 없음

 

그러나 logistic regression은 쉽게 이해하기 어렵고 decision tree는 쉽게 이해할 수 있다.

H(X)=f(X)=XW=1/(1+e^(-z))

 

 

	SVM	linear regression	logistic regression
	margin 최대	거리를 에러값으로 봄	확률로 변환
		최소제곱법 = ∑ (wxi -yi)^2 /m	1/(1+e^(-f(x)))
binary classification		H(X)=XW	H(X)= 1/(1+e^(-z)), z=XW
cost function		평균제곱오차 = ∑ (H(xi) -yi)^2/m	엔트로피 = - ∑ (ylog(H(xi) +(1-y)log(1-H(xi)))/m
최대경사법 - optimal W		W-a*cost(W)의 편미분, cost(W)=∑ (wxi -yi)^2 /2m